Z-Buffer - the backbone of the 3-D rendering

Published on 09/05/2025

TL;DR - A Z-buffer (depth buffer) keeps, for every screen pixel, the distance to the closest object rendered so far. Any time a later fragment tries to draw to the same pixel we compare depths; only the nearer fragment survives. The idea is so simple that you can implement it in ~40 lines of vanilla JavaScript and render a spinning 3-D torus entirely out of ASCII characters.

Below I'll dissect the code behind the 3D ASCII Donut demo (GitHub), see how it builds and resets its Z-buffer each frame, and learn a few tricks (cheap lighting, parameterized surfaces, time-based animation) along the way.

Setting the stage

<pre id="output" style="font-size:7px; font-weight:bold;"></pre> <pre> gives us a fixed-width text canvas. Each pair of characters will act like a square pixel, so a 70x35 ASCII grid feels roughly VGA-sized.

The user changes four parameters with range sliders:

outer radius R         // distance from donut centre to tube centre
inner radius r         // radius of the tube itself
outerCoverage (θ_max)  // how much of the big circle to draw
innerCoverage (φ_max)  // how much of the small circle to draw

Any time a slider moves we call refreshSizes(), which:

Re-reads the four inputs.
Computes size = 2 x (R + r) + 10 - a safe bounding box that fits the torus plus some margin.
Allocates zBuffer[size][size] and fills it with zeroes.

We use a full 2-D array instead of a 1-D list because the math is easier to read and JavaScript's optimizer doesn't really care at these sizes.

Marching around the torus surface

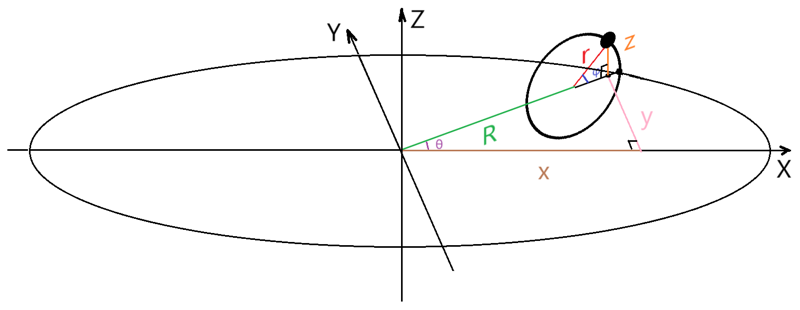
A torus is the Cartesian product of two circles:

φ runs around the tube.
θ spins that tube around the big circle.

For each (φ, θ) pair we calculate the 3-D point:

x = (R + r cos φ) cos θ
y = (R + r cos φ) sin θ
z = r sin φ

In code:

for (let φ = 0; φ <= φ_max; φ += innerStep) {
  const radius = R + r * Math.cos(φ);
  const z      = r * Math.sin(φ);

  for (let θ = 0; θ <= θ_max; θ += outerStep) {
    const x = radius * Math.cos(θ);
    const y = radius * Math.sin(θ);
    // …
  }
}

innerStep and outerStep are chosen so we take about size / 5 samples along each ring—enough that no holes appear at the current font size.

Two tiny rotations = one relaxed camera

Instead of a full view matrix we fake a camera by rotating the torus around two axes:

// spin around x-axis
const y1 = y * cos(α) - z * sin(α);
const z1 = y * sin(α) + z * cos(α);

// then around z-axis (like a top-down turntable)
const x2 =  x       * cos(β) - y1 * sin(β);
const y2 =  x       * sin(β) + y1 * cos(β);

α and β (called xyPlaneAngle and projectionRotationAngle in the demo) are slowly incremented every frame so the donut tumbles in space.

Perspective-ish projection

Because we're rendering to ASCII we can cheat: a simple orthographic projection with a depth bias is enough to feel 3-D.

const screenX = Math.round(x2) + size / 2;
const screenY = Math.round(y2) + size / 2;
const depth   = z1 + size;     // make every z positive

Now each sample knows where it wants to land in the output grid and how far away it is.

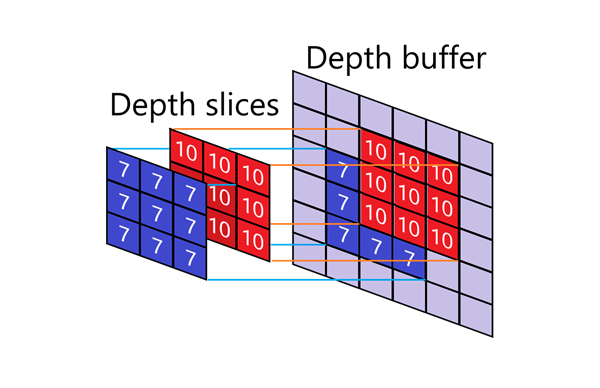
The heartbeat - Z-buffer test

if (depth > zBuffer[screenY][screenX]) {
    zBuffer[screenY][screenX] = depth;
}

At the start of the frame every Z entry is zero.
Only the point with the greatest depth value survives (remember we added size, so numerically larger depth ≈ closer to camera).
We don't store color yet-just the depth.

That single if implements hidden-surface removal: whichever bit of torus is closest to the viewer wins.

Depth buffer — The basic illustration of Z-Buffer (or depth buffer)

Converting depth differences into brightness

After all samples are processed we walk through the finished Z-buffer:

let angleCoeff = 2*z - zBelow - zRight;
angleCoeff     = (size * angleCoeff) / 12;
angleCoeff     = clamp(round(angleCoeff), 0, gradient.length‑1);

angleCoeff roughly measures the local slope: front faces differ less from neighbors than side faces, so the value is small for "bright" areas and large for "dark" ones.

Finally we index into a tiny luminance gradient:

const gradient = ['.', '"', '?', '%', '%', '#', '@'];
s += gradient[angleCoeff] + gradient[angleCoeff];

Duplicating the character horizontally re-squares the aspect ratio (most monospaced glyphs are taller than they are wide).

Animation loop

setInterval(() => {
  if (frame % 10 === 0) {          // every 10 frames shake things up
      incα = 0.03 + Math.random()/10;
      incβ = (Math.random() - 0.5)/10;
  }
  α += incα;
  β += incβ;
  renderTorus(α, β);
  ++frame;
}, 20);

20 ms per tick ≈ 50 FPS. Every ten frames we randomize the angular velocities so the motion feels organic.

renderTorus flushes output.innerText with the freshly-drawn string, the <pre> repaints, and the donut spins on.

Why the Z-buffer scales

Even in a "real" rasterizer the logic is essentially the same:

Initialize a 2-D depth array once per frame.
For every triangle fragment, compare its interpolated depth to the stored depth.
Keep the nearer fragment and optionally write color.

Complexity is O(pixels) - independent of scene geometry density - which is why Z-buffering conquered graphics hardware in the 1990s and still reigns today.

Our toy swaps triangles for parametric samples, colors for ASCII glyphs, but relies on the exact same hidden-surface test.

Takeaways

A Z-buffer is the simplest, most reliable hidden-surface algorithm.
You don't need matrices, shaders or GPUs to appreciate it - a <pre> tag and 100 lines of JS suffice.
Post-processing (slope-based brightness, double-width glyphs) sells the illusion of continuous shading.

Next time you watch a AAA game or scroll Google Maps in 3-D remember: every frame, billions of fragments still perform that humble depth comparison we just coded in one if.