Solving a tricky OA problem related to server clustering

Published on 03/04/2025

Today I came across an interesting algorithmic problem.

The problem

Initially, all applications are deployed on n servers, with varying load handling capacities. The developers want to divide the n servers into clusters of cluster_size each such that the servers in each cluster have the same load-handling capacity. To achieve this, developers can recalibrate one or more servers. In one move, any server can be reconfigured to handle a lesser load than its current capacity, i.e., in one move capacity[i], can be changed to any integer value less than capacity[i].

Given the initial capacities of the servers, in an array, capacity, of size n, and an integer cluster size, find the minimum number of moves required to divide the servers into clusters.

Example

Consider n = 6, capacity [4, 2, 4, 4, 7, 4], cluster_size = 3.

An optimal solution is shown.

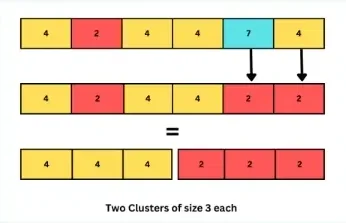
At least 2 moves are required to obtain clusters of size 3 each.

Function Description

Complete the function getMinimum Moves in the editor below.

getMinimum Moves has the following parameters:

int capacity[n]: the initial load-handling capacity of the servers

int cluster_size: the size of each cluster

Return

int: minimum moves to divide the n servers into clusters as mentioned above

Constraints

1 ≤ n ≤ 2 * 10⁵

1 ≤ capacity[i] ≤ 10⁹

1 ≤ cluster_size ≤ n

n is a multiple of cluster size

The approach

Sort the capacities by ascending order.
Maintain a priority queue for frequencies of capacities, will be explained later.
The initial value of the result (let's call it requiredMoves) will be the capacities count, will be explained later.
Start processing from the smallest capacity in clusterSize chunks.
Calculate the maximum possible capacity for each chunk (it will be the smallest capacity in that chunk).
1. In the priority queue add frequencies of capacities that are less or equal to the calculated maximum possible capacity in the current chunk. We don't add the already added frequencies again. So you have to maintain some kind of cursor and increase it when adding the capacity.
2. Pick from that priority queue the capacities with the highest frequency. You can pick at most clusterSize from that capacities. Let's name the number of that picked capacities as maxAmountToTransfer.
3. Subtract maxAmountToTransfer from requiredMoves.
4. Subtract maxAmountToTransfer from the picked capacities and update the priority queue.
Return the final value of requiredMoves.

Complexity

Time complexity: O(n * log(n))
Space complexity: O(n) (worst case)

Code (JavaScript)

This code uses OrderedMap Because JavaScript doesn't have ordered map. Please include the its code when running it in your environment.

function getMinimumMoves(capacities, clusterSize) {
	if (!capacities?.length) {
		return 0;
	}

	// sort in ascending order
	capacities.sort((a, b) => a - b);

	// OrderedMap is similar to JS map except its keys are sorted.

	// please download the source code from here
	// https: //www.npmjs.com/package/ordered-map-suren?activeTab=code
	// initialize ordered map where the keys are sorted in the descending order by the frequency
	const frequenciesPriorities = new OrderedMap((a, b) => {
		if (a.frequency !== b.frequency) {
			return b.frequency - a.frequency;
		}

		// just add a second comparison in order to avoid overriding as a duplicate
		return b.capacity - a.capacity;
	});

	requiredMoves = capacities.length;

	let lastCapacityIndex = 0,
		lastCapacity = capacities[0],
		lastCapacityFrequency = 0;

	for (let i = 0; i < capacities.length; i += clusterSize) {
		// calculate each cluster max possible capacity, it will be the minimum value of capacities
		let clusterMaxPossibleCapacity = capacities[i];

		for (let j = 1; j < clusterSize; ++j) {
			if (capacities[i + j] <
				clusterMaxPossibleCapacity) {
				clusterMaxPossibleCapacity = capacities[i + j];
			}
		}

		// add the available items to the priority queue
		while (lastCapacityIndex < capacities.length && capacities[lastCapacityIndex] <=
			clusterMaxPossibleCapacity) {
			++lastCapacityFrequency;
			const isLast = lastCapacityIndex >=
				capacities.length - 1;
			const next = isLast ? null : capacities[lastCapacityIndex + 1];

			if (isLast || lastCapacity !== next) {
				frequenciesPriorities.set({
					frequency: lastCapacityFrequency,
					capacity: lastCapacity,
				}, lastCapacity);

				lastCapacityFrequency = 0;
				lastCapacity = next;
			}

			++lastCapacityIndex;
		}

		// pick the highest priority item
		const key = frequenciesPriorities.getNthKey(0);

		if (key) {
			const maxAmountToTransfer = Math.min(key.frequency, clusterSize);
			requiredMoves -= maxAmountToTransfer;

			const newFrequency = key.frequency - maxAmountToTransfer;
			//delete it from the priority
			frequenciesPriorities.delete(key);

			// if there are capacities left update and add to the queue again
			if (newFrequency) {
				key.frequency = newFrequency;
				frequenciesPriorities.set(key, newFrequency);
			}
		}
	}

	return requiredMoves;



}

function getMinimumMoves(capacities, clusterSize) {
	if (!capacities?.length) {
		return 0;
	}

// sort in ascending order
	capacities.sort((a, b) => a - b);

// OrderedMap is similar to JS map except its keys are sorted.

// please download the source code from here
	// https: //www.npmjs.com/package/ordered-map-suren?activeTab=code
	// initialize ordered map where the keys are sorted in the descending order by the frequency
	const frequenciesPriorities = new OrderedMap((a, b) => {
		if (a.frequency !== b.frequency) {
			return b.frequency - a.frequency;
		}

// just add a second comparison in order to avoid overriding as a duplicate
		return b.capacity - a.capacity;
	});

requiredMoves = capacities.length;

let lastCapacityIndex = 0,
		lastCapacity = capacities[0],
		lastCapacityFrequency = 0;

for (let i = 0; i < capacities.length; i += clusterSize) {
		// calculate each cluster max possible capacity, it will be the minimum value of capacities
		let clusterMaxPossibleCapacity = capacities[i];

for (let j = 1; j < clusterSize; ++j) {
			if (capacities[i + j] <
				clusterMaxPossibleCapacity) {
				clusterMaxPossibleCapacity = capacities[i + j];
			}
		}

// add the available items to the priority queue
		while (lastCapacityIndex < capacities.length && capacities[lastCapacityIndex] <=
			clusterMaxPossibleCapacity) {
			++lastCapacityFrequency;
			const isLast = lastCapacityIndex >=
				capacities.length - 1;
			const next = isLast ? null : capacities[lastCapacityIndex + 1];

if (isLast || lastCapacity !== next) {
				frequenciesPriorities.set({
					frequency: lastCapacityFrequency,
					capacity: lastCapacity,
				}, lastCapacity);

lastCapacityFrequency = 0;
				lastCapacity = next;
			}

++lastCapacityIndex;
		}

// pick the highest priority item
		const key = frequenciesPriorities.getNthKey(0);

if (key) {
			const maxAmountToTransfer = Math.min(key.frequency, clusterSize);
			requiredMoves -= maxAmountToTransfer;

const newFrequency = key.frequency - maxAmountToTransfer;
			//delete it from the priority
			frequenciesPriorities.delete(key);

// if there are capacities left update and add to the queue again
			if (newFrequency) {
				key.frequency = newFrequency;
				frequenciesPriorities.set(key, newFrequency);
			}
		}
	}

return requiredMoves;

}
console.log('Running');
let result = '';

function test(p1, p2) {
	result += `capacity = [${p1.join(', ')}], cluster = ${p2} -> ${getMinimumMoves(p1, p2)} changes \n`;
}

test([1,2,2,3,4,5,5,6], 4);
test( [1,1,3,2], 2);
test( [5, 4, 2, 7, 1, 1, 5, 3, 4, 7, 4, 3, 6, 2, 1, 7, 5, 7, 5, 6, 5, 2, 1, 1, 1, 3, 4, 1, 7, 3], 5);
test( [1,2,2,2,2,3] , 3);
test([1, 1, 3, 2], 2);
test([1,2,3,4,4,5,5,6,6], 3);
test([4, 2, 4, 4, 7, 4],  3)
alert(result);