How to arrange N queens in O(N) time

Published on 16/07/2025

The definition of the problem

N Queens is a famous problem in math and computer science. It's also a popular question in leetcode / coding interviews. The N Queens problem is about arranging N queens on a chess board of NxN size in such a way that no queen attacks ony other queen. Since queens can move / attack horizontally, vertically and diagonally, no row, column and diagonal can contain more than 1 queen.

For example, for 4 queens on a 4x4 board one of the possible arrangements is this:

The N Queens problem has different flavors. Some are about counting or even outputting all the possible solutions for a given N. Some are about finding just one solution which I will discuss here.

The algorithm

One popular way to place N queens is to use some sort of backtracking algorithm which will try to examine all the possible combinations until a solution is found. The algorithm can be optimized significantly by skipping branch exploration when the current queen is already attacking other queens, even if not all queens have been placed. But even with good heuristics, the algorithm's running time still tends to grow exponentially. However, this is often the expected solution in programming interviews since they test your skills in backtracking, despite its inefficiency in finding only one solution.

Another interesting solution is Min-conflicts algorithm, which I can discuss another time. It generally works much faster and allows random solutions, but it's probabilistic and has no guarantees in time complexity.

Instead I'll discuss a simple deterministic algorithm that constructs a solution using a staircase pattern.

The staircase pattern algorithm

If you experiment with arranging N queens you might notice that when you try to arrange queens in a 3:2 staircase pattern there are usually few if any conflicts. Sometimes you just need to shift some queens horizontally or vertically and swap / change few queens' positions in order to fully eliminate the remaining conflicts. You are not mistaken if you came to a similar conclusion. There is a deterministic way to arrange N queens in a staircase pattern (with some small tweaks for some cases). Except for N = 2 and N = 3 (there are no solutions for these), you only need to handle 3 cases:

If the remainder of N divided by 6 is not 2 or 3, starting from the first row we first place queens in even positions (2, 4, 6, ...) and then in odd positions (1, 3, 5, ...). Examples:

6 queens

7 queens
If the remainder of N divided by 6 is 2, like in the previous case, starting from the first row we place queens in even positions (2, 4, 6, ...). But for odd positions we need to do some tweaks. In the next 2 rows we place queens in the 3rd and the 1st positions. Then, in the following rows, we place queens in odd positions starting from 7 (7, 9, 11, ...). And, finally, in the last row, we place the last queen in the 5th remaining position. Example: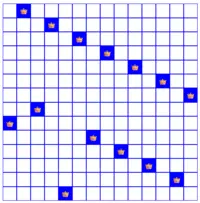

14 queens
If the remainder of N divided by 6 is 3, we need to do something a bit different. Starting from the first row we place queens in even positions, but skipping the 2nd position (4, 6, 8, ...). In the following row we place a queen in that skipped 2nd position. Then, in the following rows, we place queens in odd positions starting from 5 (5, 7, 9, ...). And, finally, in the last 2 rows, we place the last queens in the 1st and 3rd remaining positions. Example: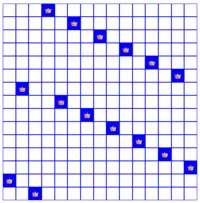

15 queens

This isn't too hard to prove, when Nis incremented by 6 the relative offsets of queens' occupied diagonals remain similar. So if this works from 4 to 9, it will work from 4 + 6 to 9 + 6, etc. The algorithm works in O(N) or O(N²) time, depending on the output format (row position indexes or the whole NxN matrix).

Code (JavaScript)

function nQueensInLinearTime(n) {
	if (n !== 1 && n < 4) {
		return Array.from({ length: n }, () => -1);
	}

	const ans = [];

	if (n % 6 === 3) {
		for (let i = 3; i < n; i += 2) {
			ans.push(i);
		}

		ans.push(1);

		for (let i = 4; i < n; i += 2) {
			ans.push(i);
		}

		ans.push(0, 2);
	} else if (n % 6 === 2) {
		for (let i = 1; i < n; i += 2) {
			ans.push(i);
		}

		ans.push(2, 0);

		for (let i = 6; i < n; i += 2) {
			ans.push(i);
		}

		ans.push(4);
	} else {
		for (let i = 1; i < n; i += 2) {
			ans.push(i);
		}

		for (let i = 0; i < n; i += 2) {
			ans.push(i);
		}
	}

	return ans;
}

Playground

Here you can change the N with the slider and immediately see the staircase pattern. Better to see something once than to hear about it a thousand times:

Please enable JavaScript if you want to visualize the solutions for N Queens.

0 queens

Conclusion

This is a simple but often overlooked trick to solving the N Queens problem. The next time an interviewer asks you to write a program that will arrange N queens, you can also show him this solution along with the standard backtracking solution.