Leetcode Pens and Pencils problem in O(log(n)) time

Published on 27/03/2025

There is a leetcode problem Number of Ways to Buy Pens and Pencils. It has the following requirement:

You are given an integer total indicating the amount of money you have. You are also given two integers cost1 and cost2 indicating the price of a pen and pencil respectively. You can spend part or all of your money to buy multiple quantities (or none) of each kind of writing utensil.

Return the number of distinct ways you can buy some number of pens and pencils.

Example 1:

Input: total = 20, cost1 = 10, cost2 = 5
Output: 9
Explanation: The price of a pen is 10 and the price of a pencil is 5.
- If you buy 0 pens, you can buy 0, 1, 2, 3, or 4 pencils.
- If you buy 1 pen, you can buy 0, 1, or 2 pencils.
- If you buy 2 pens, you cannot buy any pencils.
The total number of ways to buy pens and pencils is 5 + 3 + 1 = 9.

Example 2:

Input: total = 5, cost1 = 10, cost2 = 10
Output: 1
Explanation: The price of both pens and pencils are 10, which cost more than total, so you cannot buy any writing utensils. Therefore, there is only 1 way: buy 0 pens and 0 pencils.

The naive solution

The naive solution will look like this:

long long result = 0;
while (total >= 0) {
	result += total / cost2 + 1;
	total -= cost1;
}
return result;

It calculates for each number of item 1 the possible number of item 2 and sums the results. The worst case execution time would be O(total/max(cost1,cost2)) if we optimize by subtracting the greatest of cost1 and cost2 from total, but it is still linear (proportional to total) in the worst case.

Can we do faster? It turns out yes.

The problem is equivalent to a geometrical problem of finding the number of discrete points that satisfy these conditions:

cost1 * x + cost2 * y ≤ total
x ≥ 0
y ≥ 0
x is a whole number
y is a whole number

For 11x + 17y ≤ 40 the graphical representation will be like this:

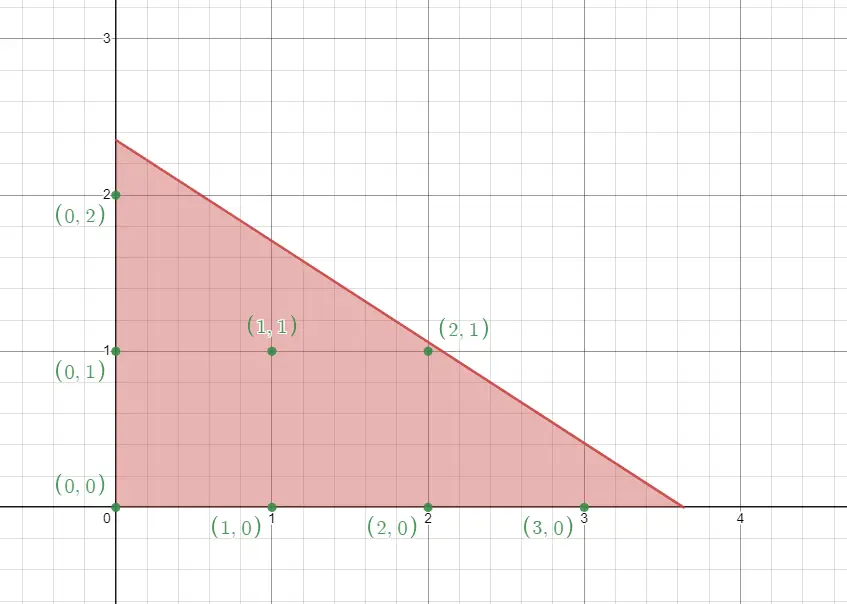
The red triangle contains 8 points (including the ones that touch its sides) that have integer (whole) coordinates.

So how can we quickly find the number of such points in any triangle?

A better approach

We can calculate the total amount of points by taking the advantage of the fact that we can calculate the number of the points in a triangle with legs a and k*a in a constant amount of time, where k is a whole number and a is positive number (can be non whole number too).

Let's consider a triangle with k=2:

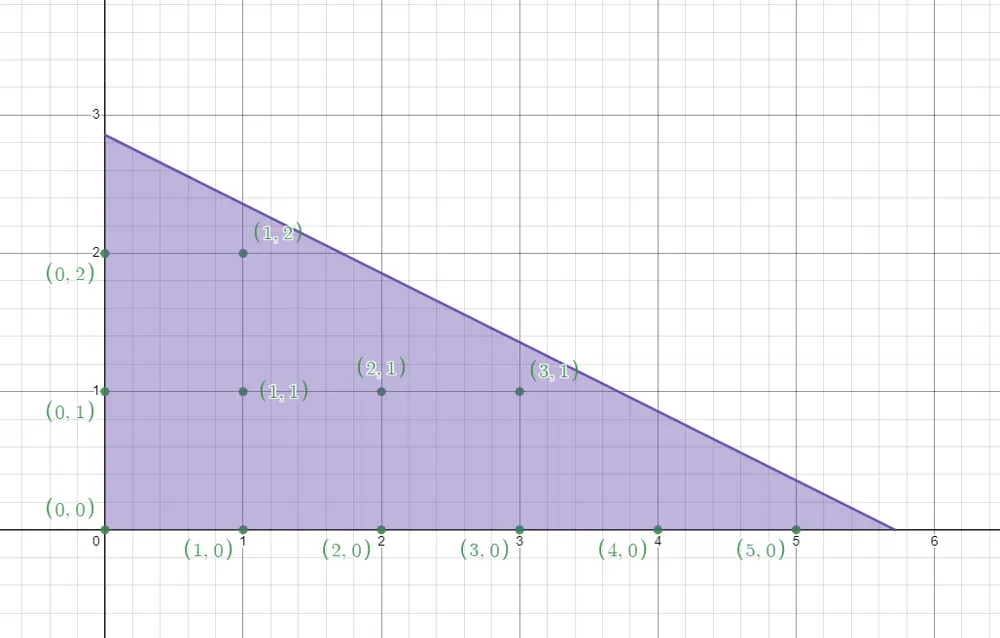
We can easily calculate the number of points within a constant amount of time with the help of arithmetic progression formula (S = (a₁ + a_n) * n / 2), since every next (upper) row has k (in this example 2) less points than the previous one and we can calculate the number of elements and the points in the bottom row in a constant amount of time by integer division / rounding. I.e. it's 6 + 4 + 2 = (6 + 2) * 3 / 2 = 12 in this case.

OK, but not all cases will be triangles with legs of a and a*k, so how can we count for any triangle? Yes, not all triangles are like this, but we can extract such triangle from any triangle and transform the remaining figure to a smaller triangle and repeat this process until the remaining figure is small enough to calculate its points in a constant amount of time.

This is how it works

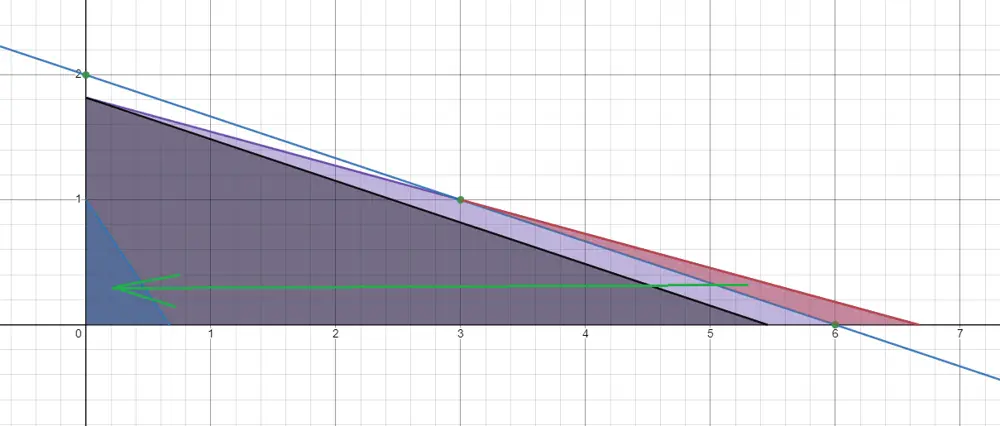
The pink triangle (it's the largest triangle, only small part is visible) is the original one. BTW, The pink triangle is always normalized so that its width is always more then or equal to its height.
The gray one shares the smallest leg with the original one. Its other leg is the largest multiple of the smallest leg that fits in the original triangle's largest leg (k=3 in this example)
The blue line is parallel to the hypotenuse of the gray triangle and passes through the closest integer points (from the right), if the gray triangle hypotenuse passes through integer points the blue line should pass through the next closest (right) integer points.
The red triangle is the part of the original triangle that is above the blue line.
Since the blue line passes through points with integer coordinates the red triangle can be safely transformed (preserving the number of the points with integer coordinates) to the blue triangle with a horizontal skew.
The total points in the original triangle will be the number of the points in the gray triangle + the number of points in the red triangle (or the blue triangle, since it preserves the red triangle points' number). The area between the hypotenuse of the gray triangle and blue line (looks pink in the picture) cannot contain any point with integer coordinates.
So, in order to calculate the total points with integer coordinates, we need to calculate the total points of the gray triangle (const time) and recursively calculate the point number of the blue triangle.

Since in each iteration one of the sides of the next triangle decreases by a factor of at least 2 (similar to Euclidean algorithm), the complexity will be logarithmical in the worst case.

When we have cost1, cost2, cost1 ≤ cost2 (the horizontal leg shouldn't be smaller than the vertical leg, otherwise we swap cost1 and cost2) and total, the figures will have such properties:

The pink triangle that satisfies the condition cost1 * x + cost2 * y ≤ total will have width (horizontal leg length) w = total / cost1 and height (vertical leg length) h = total / cost2.
k = floor(w / h) = floor((total / cost1) / (total / cost2)) = floor(cost2 / cost1).
The integer part of the height will be n = floor(h) = floor(total / cost2). The number of integer coordinates in the vertical leg will be n + 1.
The number of integer coordinates in the base of the gray triangle will be l = floor(k * h) + 1 = floor(k * total / cost2) + 1.
The number of points with integer coordinates in the gray triangle will be a sum of an arithmetic progression: S = (a₁ + a_n+1) * (n + 1) / 2 = (l + l - k * n) * (n + 1) / 2 = (n + 1) * (2 * l - k * n) / 2.
The X coordinate of the intersection of the blue line and X axis will be floor(k * h) + 1 = l.
The Y coordinate of the intersection of the blue line (this is also the length of the vertical leg of the blue triangle) and the hypotenuse of the pink triangle after solving the linear equation will be (total - cost1 * l) / (cost2 - cost1 * k) (for now ignore the case where the denominator is 0).
The horizontal leg of the blue triangle (also the base of the red triangle, since the blue triangle was the result of the red triangle horizontal skewing) will be w - l = total / cost1 - l = (total - cost1 * l) / cost1.
Just notice that for both horizontal and vertical legs' lengths of the blue triangle the numerator is total - cost1 * l. This means that the blue triangle can be considered as a smaller version of the original problem with this parameters:
- total_new = total - cost1 * l
- cost1_new = cost2 - k * cost1
- cost2_new = cost1
This trick also eliminates the need for division. So it will not cause any problems even when some of the denominators are 0. We will always check if total is large enough proportionally to cost2 in order to continue to compute the result recursively or just fall back to the "naive" approach. total_new can even be negative, but the algorithm will still work correctly. It might be not that obvious but it is true.

Complexity

Time complexity: O(log(min(cost1,cost2,total))) (worst case)
Space complexity: O(1)

Code (C++)

class Solution {
public:
	long long waysToBuyPensPencils(int total, int cost1, int cost2) {
		if (cost2 < cost1) {
			swap(cost1, cost2);
		}

		long long res = 0;

		while (true) {
			if (4 * cost2 > total) {
				while (total >= 0) {
					res += total / cost1 + 1;
					total -= cost2;
				}

				return res;
			}

			auto k = cost2 / cost1;
			auto n = total / cost2;
			auto l = k * total / cost2 + 1;

			res += (long long)(n + 1) * (2 * l - k * n) / 2;

			total -= cost1 * l;
			auto temp = cost2;
			cost2 = cost1;
			cost1 = temp - k * cost1;
		}
	}
};

I also posted this solution here.